Phase-field approach for crack modeling:
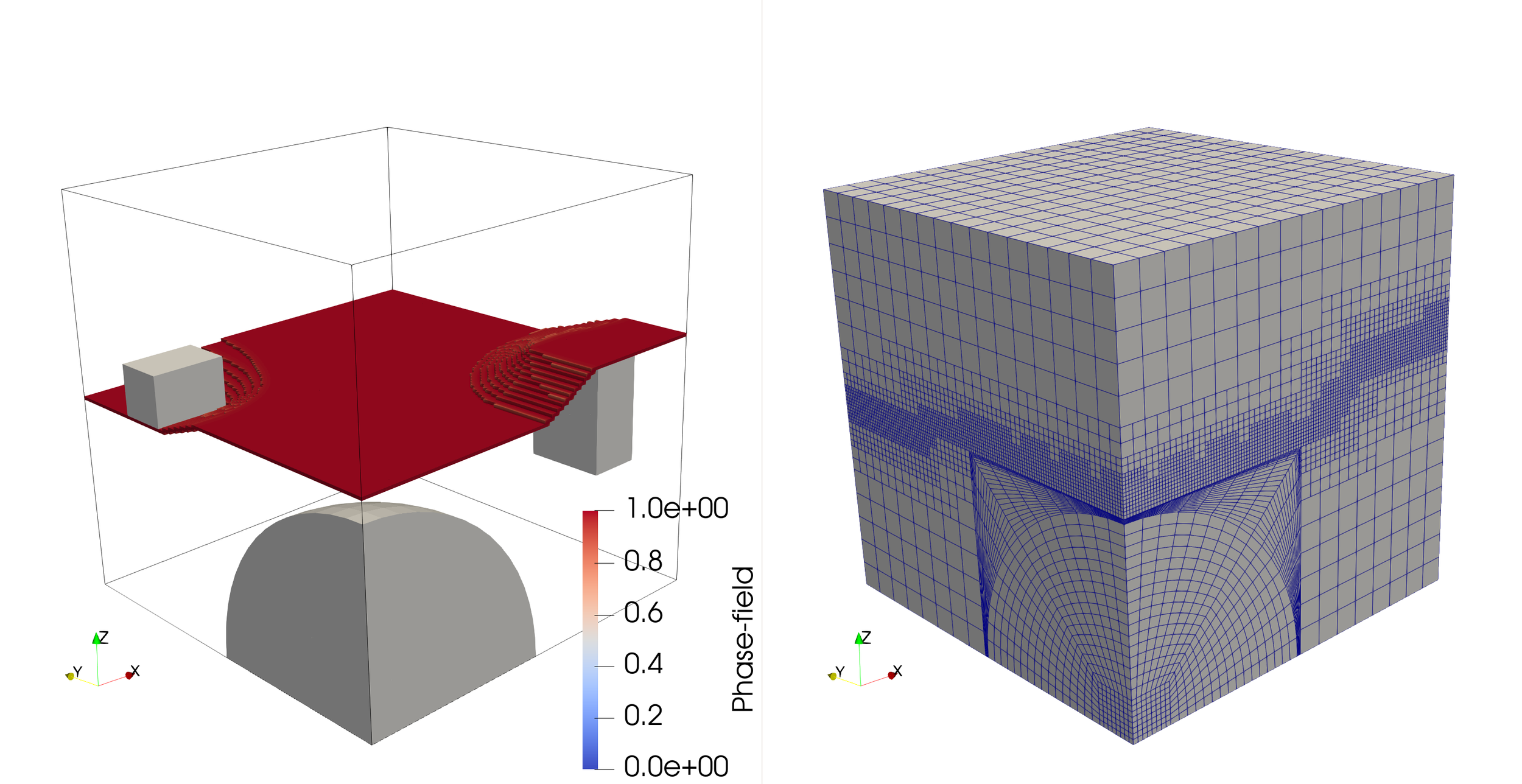
Fig 1. Crack propagation inside a material sample containing two rigid body inclusions. The L-BFGS monolithic solver combined with an adaptive mesh refinement technique makes the phase-field approach practical for 3D simulations.
Fig 2. Crack propagation inside a concrete beam under torsion. The crack surface represented by the phase-field is non-planar.
Background and motivation: Many numerical approaches rely on heuristic tracking algorithms to track the crack propagation path during crack simulations, which only find limited successes in relatively simple cases. In recent years, the phase-field approach becomes a popular choice for crack modeling due to its capability of naturally handling complex crack patterns such as merging and branching in both 2D and 3D problems. However, the phase-field crack modeling faces the following three challenges. First, the total energy functional of a cracked solid is non-convex. As a result, classical Newton-based approaches encounter convergence issues during nonlinear iterations. Second, the phase-field modeling is intrinsically expensive, since highly refined meshes need to be used near the crack region. Third, the phase-field modeling needs to enforce the so-called irreversibility condition to prevent crack from self-healing.
In this research, we developed a series of the limited-memory BFGS (L-BFGS) monolithic approaches to solve the phase-field crack problem. These approaches can overcome the convergence difficulties arising from the non-convexity of the total energy functional, and therefore, significantly improve the robustness of the FE simulations. Also, an adaptive mesh refinement strategy is incorporated into the L-BFGS monolithic solver, which limits the use of highly refined meshes only around the crack path. This feature makes the developed method practical for 3D simulations. Lastly, the developed method offers two different approaches to enforce the phase-field irreversibility condition, the history variable approach that is largely adopted in the literature and the gradient projection approach that strictly enforces the inequality constraints imposed on the phase-field. To support the effort of open science and reproducible research, we host our developed computer code on GitHub: https://github.com/taojinllnl.